Dies ist eine glaub ich recht elegante Formulierung der Beweise. Das Prinzip beruht auf der Flächengleichheit von Dreiecken und geht (wie fast alles !-) auf Euklid zurück:

Erster Strahlensatz
(Die Abschnitte auf beliebigen Strahlen, verursacht durch zwei Parallelen, haben immer das gleiche Verhältnis.)

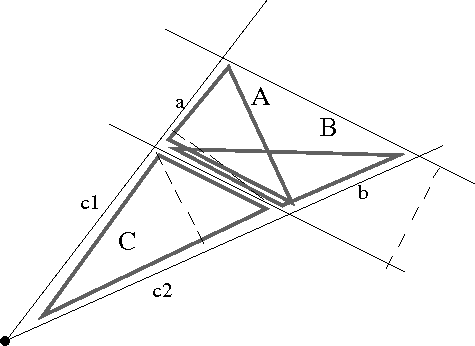
Siehe diese Figur:

Die Dreiecke A und B haben eine Grundseite und Höhe (gestrichelte Linie, nämlich genau der Abstand der zwei Parallelen) gemeinsam. Also auch den Flächeninhalt.
A und C haben die Höhe (gestrichelte Linie) gemeinsam, also verhalten sich die Strahlenabschnitte a und c1 (als die dazugehörigen Grundseiten) zueinander wie die Flächeninhalte von A und C.
B und C haben die Höhe (gestrichelte Linie) gemeinsam, also verhalten sich die Strahlenabschnitte b und c2 (als die dazugehörigen Grundseiten) zueinander wie die Flächeninhalte von B und C.
Also (da A und B gleiche Fläche haben) verhält sich a zu c1 wie b zu c2. QED

Zum zweiten Strahlensatz:
(Die Abschnitte auf den Parallelen verhalten sich wie die auf einem Strahl.)

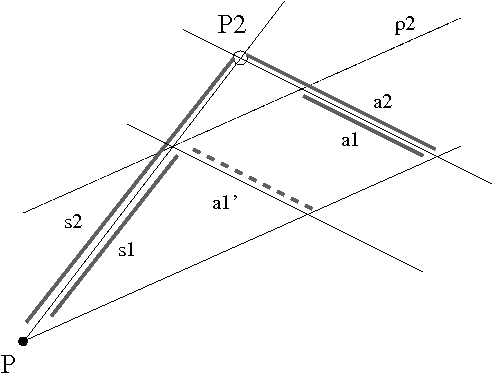
Man ergänze zusätzlich zur Ausgangsgraphik die Parallele p2 zu dem einen Strahl und wende den ersten Strahlensatz an mit dem anderen Strahl und der äußeren ursprünglichen Parallele als Strahlen (mit Schnittpunkt P2).
Dann ist nach dem ersten Strahlensatz das Verhältnis des kürzeren zum längeren Abschnitt auf diesem Strahl (s1 zu s2) gleich dem des kürzeren zum längeren Abschnitt auf dieser äußeren Parallelen (a1 zu a2).
Da die Figur in der Mitte ein Parallelogramm ist, ist der Abschnitt auf der äußeren und der inneren (ursprünglichen) Parallelen gleich lang.
Also verhalten sich die Abschnitte auf den Parallelen (a1' zu a2) wie die auf dem einen Strahl (s1 zu s2).

Zum dritten Strahlensatz:
(Beliebige Abschnitte auf den Parallelen verhalten sich gleich.)
Dazu braucht man noch nichtmal ein Bild: Wenn die Abschnitte auf den Parallelen sich wie die auf einem ausgewählten Strahl verhalten, dann verhalten sich alle Abschnitte auf den Parallelen so, also auch untereinander gleich.

© senzatempo.de     markuslepper.eu       2019-12-20_20h49          
produced with eu.bandm.metatools.d2d    and   XSLT
music typesetting by musixTeX    and   LilyPond